Activity 00309 - 01: Top Five
Subject 08675; thank you again for your participation. You are asked to answer each question as honestly and objectively as possible. To help the integrity of the research, please follow all instructions exactly as they are given.
Purpose:
To understand pair-wise comparisons, converting votes to graphical form,
converting graphs to matrices, entering data into Matlab, and importing Matlab .m files.
Materials:
Paper, writing utensil, and Matlab
Estimated Time:
20 minutes (not including downloading of .m files)
In this activity, you will be ranking your top five Internet sites. Throughout the entire lab, Subject 1 is used as our example subject. You may use any sites you choose, but should follow the same methods as Subject 1.
Instructions:
On your paper, write the letters A through E in a column. Next to each letter, list a different Internet site. Preferably, the sites should be listed in random order.
Subject 1:
A) Google
B) College of Charleston
C) MySpace
D) Internet Movie Database
E) Napster
Now rank them in the order of most hours used to least hours used. That is, if a person were to walk past and glance at your screen, what site would they most likely see?
Subject 1:
1) Napster
2) Google
3) MySpace
4) College of Charleston
5) Internet Movie Database
While you may think this is a correct ordering, the only unbiased way to rank the pages is by performing a pair-wise comparison of each page. In this way, each page "votes" for every other page. That is, suppose you use site A more than site B, then site A should cast a vote for site B.
In order to do the comparisons, list out every possible pairing of the sites. Next, circle the site you use more frequently from each pair. Again, circle the site you are most likely to be visiting at any random moment, not your favorite site.
Subject 1: (Letters in red are selected by Subject 1)
A or B B or C C or D D or E A or C B or D C or E A or D B or E A or E
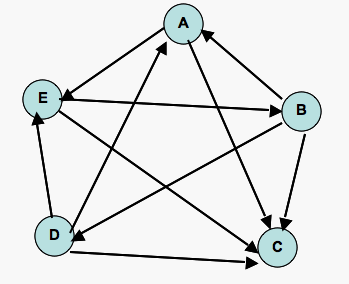
We now need to create the voting graph based on the pair-wise comparisons you made for each site. In the case of Subject 1, A was chosen over B, so an arrow points from B to A. The directedness of the arrow is important as it graphically shows the preference of each pair.
By simply counting the number of votes for each site, we would say that sites A and E tie. However, the strength of a voting site makes a difference in the "final count." For example, since site D has one vote for it, then it makes sense that its vote for site E should count less than the vote from site A (which has two votes) for site E.
Although the graph helps us visualize the connectivity of the sites, it is difficult to interpret. We need to represent the data in a mathematical way in order to find the unbiased "winner." Furthermore, a graphical comparison of millions of sites in the entire World-Wide-Web is unimaginable and infeasible.
A great way to store relational information is in a matrix. The 5x5 connectivity matrix will have the rows representing the "from" sites and the columns representing the "to" sites. So, Subject 1 will place a 0 in row A column D since there is no link from site A to site D, and a 1 in row A column E since there is a link from site A to site E.
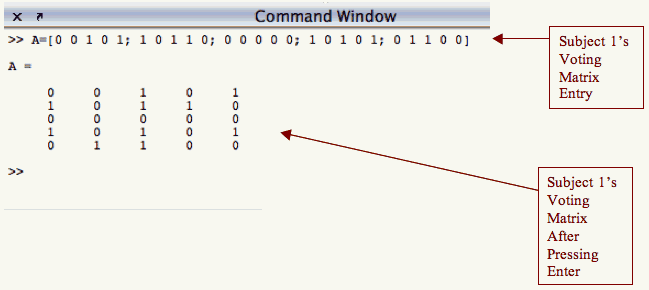
Subject 1 Voting Matrix:
A B C D E A 0 0 1 0 1 B 1 0 1 1 0 C 0 0 0 0 0 D 1 0 1 0 1 E 0 1 1 0 0
You are now ready to use the PageRank algorithm similar to the one used by Google. For now, we will have you simply enter the matrix into Matlab and use imported .m files to interpret your data. In other activities, you will learn how the Google matrix works. For help in using Matlab, you can go to this elementary tutorial.
Open your Matlab application.