Glossary
- Eigen Decomposition
- Let P be a matrix os eigenvectors of a given square matrix A, and D be a diagonal matrix with corresponding eigenvalues on the diagonal. Then, as long as P is a square matrix, A can be written as an eigen decomposition:
A = P*D*P^-1
This is also referred to as matrix diagonalization. Here, matrix A is said to be diagonalizable. Any nxn matrix is diagonalizable as long as P is invertible.
(from www.mathworld.com)
- Length (of a vector)
- If a vector v = (x, y, z), then the length of v (denoted ||v||) can be found by calculating:
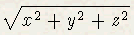
This is also called the norm of a vector.
- Orthogonal
- Two vectors are orthogonal, or perpendicular, if their inner product (or dot product) is zero.
- Polysemy
- The existence of two or more possible meanings for a word or phrase.
ex. Second can mean a unit of time or denote an item's place in a list.
- Rank
- The rank of a matrix A is the number of linearly independent rows or columns of A.
- Synonymy
- The existence of two or more terms for the same item or idea.
ex. Car and Automobile are two different words for the same thing.
- Vector Space
- A vector space V is a set that is closed under finite vector addition and scalar multiplication. In order for V to be a vector space, the following conditions must hold for elements X, Y, Z in V and scalars r and s:
- Commutativity: X+Y=Y+X
- Associativity of vector addition: (X+Y)+Z=X+(Y+Z)
- Additive identity: X+0=0+X=X
- Existence of an additive inverse: For any X, there exists a (-X) such that X+(-X)=0.
- Associativity of scalar multiplication: r(sX)=(rs)X
- Distributivity of scalar sums: (r+s)X=rX+sX
- Distributivity of vector sums: r(X+Y)=rX+rY
- Scalar multiplication identity
Get back to where you where:letter 1 2 3 4 5 6